Answer:
The mean absolute deviation = 3.5°F
Explanation:
The sum of the given temperatures, ∑T, is found as follows;
∑T = 66°F + 57°F + 61°F + 65°F + 54°F + 62°F + 59°F + 56°F = 480°F
The number of days, n, over which the temperature was tracked = 8 days
Therefore, the mean,
 , of the data set = ∑T/n = 480°F/8 = 60°F
, of the data set = ∑T/n = 480°F/8 = 60°F
The mean absolute deviation is given by the following formula;
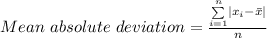
Therefore, we have;
66 - 60 =
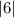 = 6
= 6
57 - 60 =
 = 3
= 3
61 - 60 =
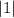 = 1
= 1
65 - 60 =
 = 5
= 5
54 - 60 =
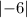 = 6
= 6
62 - 60 =
 = 2
= 2
59 - 60 =
 = 1
= 1
56 - 60 =
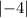 = 4
= 4
The mean absolute deviation is therefore;
The mean absolute deviation = (6 + 3 + 1 + 5 + 6 + 2 + 1 + 4)/8 = 3.5°F.