Question

In the figure below, points A, E, F, and C lie in plane X.

Points B and D do not lie in plane X.
For each part below, fill in the blanks to write a true statement.
B
(a) FC and
are distinct lines that intersect.
A.
X
C
E
F
(b) B. I, and I are distinct points that are collinear.
(c) Another name for plane X is plane I.
(d) E, I, I, and I are distinct points that are coplanar.

Answer 1

a) FC ←→ and BD ←→ are distinct lines that intersect.

b) B , C and D are distinct points that are collinear.

c) Another name for plane
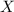`X` is plane AEF.

d) E , A , F and C are distinct points that are coplanar.

Explanation:

The first step to solve this question is to look carefully at the picture.

For a) :

We can see that the line FC and the line BD intersect at the point C.

We can write :

a) FC ←→ and BD ←→ are distinct lines that intersect (we can see more lines that intersect with FC ←→ in the picture such as AC ←→ or AE ←→).

For b) :

We can see that the line BD ←→ passes through the points B , C and D (B , C and D are collinear points).

We can write :

b) B , C and D are distinct points that are collinear.

For c) :

We can name any plane using three points which are contain in the plane but this three points must not be collinear points.

We can name the plane
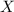`X` using the points A , E and F (this is a possible solution).

We can write :

c) Another name for plane
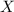`X` is plane AEF.

Finally, for d) :

Two or more points are coplanar wherever they belong to the same plane.

In the picture, the points A , E , F and C belong to the plane
`X`.

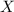We can write :

d) E , A , F and C are distinct points that are coplanar.