Question

What is the angle of elevation of the sun when a pole 32.0 ft tall casts a shadow 45.0 ft long

Answer 1

As you can see in the first drawing, the vertical line represents the pole which is 32.0 ft long and the horizontal line represents the shadow casted by the pole which is 45.0 ft long. The angle θ, represents the angle of elevation of the sun.

We can solve this problem using trigonometric ratios, that is sine, cosine, and tangent. Remember SOH CAH TOA?

SOH

`sin = (opposite)/(hypotenuse)`

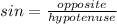
CAH

`cosine = (adjacent)/(hypotenuse)`

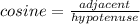
TOA

`tan = (opposite)/(adjacent)`

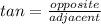
In this case, we're going to use TOA since we are given the height of the pole which represents the line opposite the angle of elevation, and the length of the shadow of the pole which represents the line adjacent to the angle of elevation.

adjacent, a = 45.0

opposite, o = 32.0

So, to find the angle of elevation, refer to the second picture above.