Question

Which statement describes the inverse of m(x) = x2 – 17x?

Answer 1

b

Explanation:

edge 2021

Answer 2

The correct option is;

`The \ domain \ restriction \ x \geq (17)/(2) \ results \ in \ m^(-1)(x) = (17)/(2) \pm \sqrt{x + (289)/(4) }}`

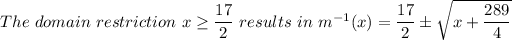
Explanation:

The given information is that m(x) = x² - 17·x

The above equation can be written in the form;

y = x² - 17·x

Therefore;

0 = x² - 17·x - y

From the general solution of a quadratic equation, 0 = a·x² + b·x + c we have;

`x = \frac{-b\pm \sqrt{b^(2)-4\cdot a\cdot c}}{2\cdot a}`

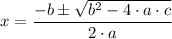
By comparison to the equation,0 = x² - 17·x - y, we have;

a = 1, b = -17, and c = -y

Substituting the values of a, b and c into the formula for the general solution of a quadratic equation, we have;

`x = \frac{-(-17)\pm \sqrt{(-17)^(2)-4* (1) * (-y)}}{2* (1)} = (17\pm √(289+4\cdot y))/(2)`

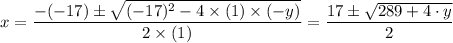
Which can be simplified as follows;

`x = (17\pm √(289+4\cdot y))/(2)= (17)/(2) \pm (1)/(2) * √(289+4\cdot y)} = (17)/(2) \pm \sqrt{(289)/(4) +(4\cdot y)/(4) }}`

And further simplified as follows;

`x = (17)/(2) \pm \sqrt{(289)/(4) +y }} = (17)/(2) \pm \sqrt{y + (289)/(4) }}`

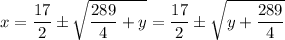
Interchanging x and y in the function of the inverse, m⁻¹(x), we have;

`m^(-1)(x) = (17)/(2) \pm \sqrt{x + (289)/(4) }}`

We note that the maximum or minimum point of the function, m(x) = x² - 17·x found by differentiating the function and equating the result to zero, gives;

m'(x) = 2·x - 17 = 0

x = 17/2

Similarly, the second derivative is taken to determine if the given point is a maximum or minimum point as follows;

m''(x) = 2 > 0, therefore, the point is a minimum point on the graph

Therefore, as x increases past the minimum point of 17/2, m⁻¹(x) increases to give;

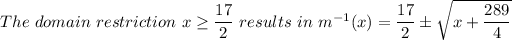`The \ domain \ restriction \ x \geq (17)/(2) \ results \ in \ m^(-1)(x) = (17)/(2) \pm \sqrt{x + (289)/(4) }}` to increase m⁻¹(x) above the minimum.