Answer:
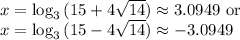
Explanation:
So we have the equation:
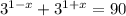
First, note that this is the same as:
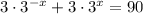
Factor out a 3:
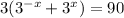
Divide both sides by 3:
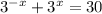
Change the negative exponent into a fraction:
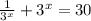
Multiply both sides by 3^x:
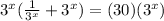
Distribute:
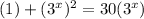
Let u equal 3^x. So:
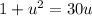
Subtract 30u from both sides:
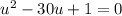
This is a quadratic. Solve using the quadratic formula. A is 1, b is -30, and c is 1. So:
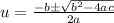
Substitute:
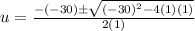
Simplify:
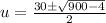
Subtract:
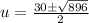
Simplify:
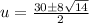
Simplify:
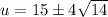
Substitute back u:
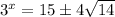
Take the log to base 3 of both sides:
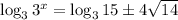
The left side cancels:
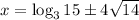
So, our solutions are:
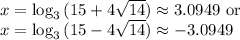
And we're done!