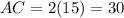Answer:

Explanation:
First, we know that the entire segment adds up to 5(2x+2). In other words:
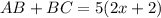
Now, since B is the midpoint of AC, by the definition of midpoint, AB and BC are equivalent. So:
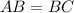
Since we know that, let's substitute BC for AB in the first equation:
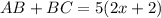
This is equivalent to:
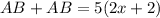
Combine like terms:
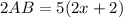
And since we know that AB is 3(3x-1), substitute:
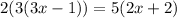
Now, solve for x.
Distribute the left side:

Distribute both sides:

Add 6 to both sides:
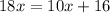
Subtract 10x from both sides:
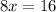
Divide both sides by 8:

So, the value of x is 2.
And we're done!
Notes:
You didn't particularly state what you need to find. If you want to length of AB or BC, it would be:
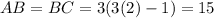
And the entire length AC is: