Question

One sample has a mean of M=7.2 and a second sample has a mean of M=12.8. The two sample are combined into a single set of scores. a. What is the mean for the combined set if both the samples have n=5? b. What is the mean for the combined set if the first sample has n=5 and the second sample had n=35?

Answer 1

a. M = 50

b. M = 242

Explanation:

mean =
`(sum of scores)/(number of samples)`

⇒ sum of scores = mean x number of samples

Let the mean be represented by M, and the number of samples be represented by n,

sum of scores = M x n

a. When n = 5 for both samples,

The first sample's sum of scores = M x n

= 7.2 x 5

= 36

The second sample's sum of scores = M x n

= 12.8 x 5

= 64

The mean for the sum of scores of the combined set =
`(36 + 64)/(2)`

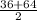
= 50

When both samples have n = 5, the mean of the combined set is 50.

b. When the first sample has n = 5, the sum of scores = 36.

If n = 35 for the second sample, the sum of scores = M x n

= 12.8 x 35

= 448

The mean for the sum of scores of the combined set =
`(36 + 448)/(2)`

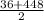
= 242