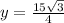Answer:
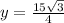
Explanation:
Well what you have here are two right triangles within another right triangles created by an altitude. This results in 3 similar triangles (see attached for reference)
As a result , using the properties of similar triangles, and taking ratios of their sides of the medium triangle and the largest triangle, we can form the following relationship:
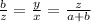 (we know that a+b = 15), hence the equation becomes:
(we know that a+b = 15), hence the equation becomes:
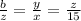 ----------eq 1
----------eq 1
If we consider the largest triangle, we will see that
cos 30° = z / 15
but from our special angles (see second attachment) we know that cos 30° = (√3)/2
hence
(√3)/2 = z / 15
z = (15√3) / 2 --------eq 2
from the same largest triangle, we will also see that
sin 30° = x / 15
similarly from our special angles, we know that sin 30° = 1/2
hence,
1/2 = x/15
x = 15/2 --------eq 3
now that we have values for x and z, we can neglect the first term of equation 1 and form an equality with x, y and z
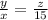
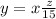 (substituting the values for x and z that we found above)
(substituting the values for x and z that we found above)
y = (15/2) · [ (15√3) / 2] / 15
y = (15√3) / 4