Answer:
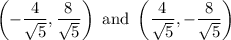 .
.
Explanation:
We need to find all the points on the curve x=4cos(t),y=4sin(t) that have the slope of 1/2.
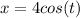
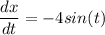
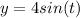
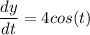
Now,
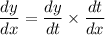
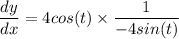
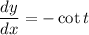
So, slope of the curve is
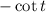 .
.
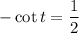
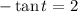
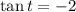 ...(1)
...(1)
Using
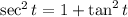 , we get
, we get
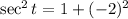
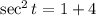
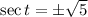
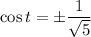
Now,
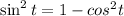
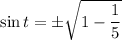
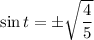
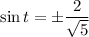
It equation (1), tan(t) is negative. So, sin and cos have different signs.
If
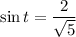 , then
, then
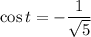 .
.
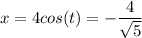
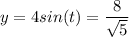
If
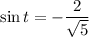 , then
, then
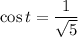 .
.
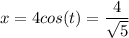
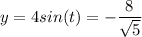
Therefore, the two points are
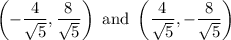 .
.