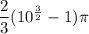Question

Find the area of the surface. The part of the surface z = xy that lies within the cylinder x^2 + y^2 = 9

Answer 1

The area of surface is
`(2)/(3)(10^{(3)/(2)}-1)\pi`

Explanation:

Given that,

The equation of cylinder is

`x^2+y^2=9`

The part of the surface z = xy

The coordinates is,

`z_(x)=y`

`z_(y)=x`

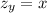
We need to calculate the value of ds

Using formula of ds

`ds=\sqrt{1+z_(x)^2+z_(y)^2}dA`

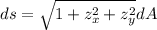
Put the value in to the formula

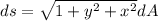`ds=√(1+y^2+x^2)dA`....(I)

We know that.

The polar coordinates,

`x=r\cos\theta`

`y=r\sin\theta`

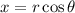
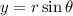
The general equation of cylinder is

`x^2+y^2=r^2`

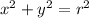
compare from given equation

`x^2+y^2=3^2`

0<=θ<=2π, 0<=r<=3

Area element in polar coordinates is,

`dA=r dr d\theta`

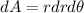
Put the value of dA in equation (I)

`ds=√(1+r^2)r dr d\theta`....(II)

We need to calculate the area of surface

Using equation (II)

`s=\int_(0)^(2\pi)\int_(0)^(3)√(1+r^2)r dr d\theta`

`s=\int_(0)^(2\pi)(1)/(3)((1+r^2)^{(3)/(2)})_(0)^(3)d\theta`

`s=\int_(0)^(2\pi)(1)/(3)((1+3^2)^{(3)/(2)}-(1+0^2)^{(3)/(2)})d\theta`

`s=((1)/(3)((10)^{(3)/(2)}-1)\theta)_(0)^(2\pi)`

`s=(1)/(3)(10^{(3)/(2)}-1)(2\pi-0)`

`s=(2)/(3)(10^{(3)/(2)}-1)\pi`

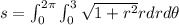
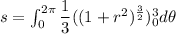
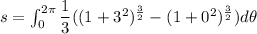
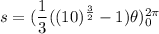
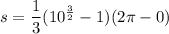
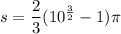
Hence, The area of surface is
`(2)/(3)(10^{(3)/(2)}-1)\pi`