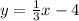Answer:
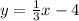
Explanation:
Step 1: Solve for y in the first equation
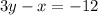
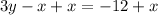
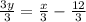
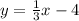
Step 2: Determine the important aspects
We know that our line is parallel to the other line that has a slope of 1/3 which means that our slope is also going to be 1/3. We also know that our line crosses the point (18, 2) which means that we can use the point slope form to determine our equation
Point Slope Form →
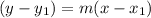
Step 3: Plug in the information and solve
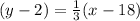
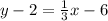
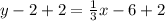
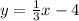
Answer: