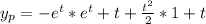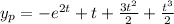Complete Question
Find a particular solution to
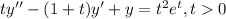
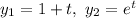
Answer:
The solution is
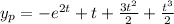
Explanation:
Now the given equation is
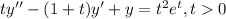
dividing through by t
We have
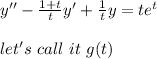
Now for the given initial value we can generate our Wronskian as follows
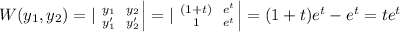
Now applying method of variation of parameters to obtain the particular solution
So here we assume that
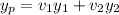
So

And
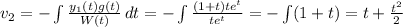
So