Question

Find the first partial derivatives of the function f(x,y,z)=4xsin(y−z)

Answer 1

`f_x(x,y,z)=4\sin (y-z)`

`f_x(x,y,z)=4x\cos (y-z)`

`f_z(x,y,z)=-4x\cos (y-z)`

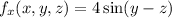
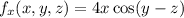
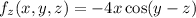
Explanation:

The given function is

`f(x,y,z)=4x\sin (y-z)`

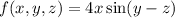
We need to find first partial derivatives of the function.

Differentiate partially w.r.t. x and y, z are constants.

`f_x(x,y,z)=4(1)\sin (y-z)`

`f_x(x,y,z)=4\sin (y-z)`

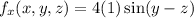
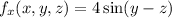
Differentiate partially w.r.t. y and x, z are constants.

`f_y(x,y,z)=4x\cos (y-z)(\partial)/(\partial y)(y-z)`

`f_y(x,y,z)=4x\cos (y-z)`

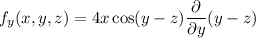
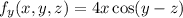
Differentiate partially w.r.t. z and x, y are constants.

`f_z(x,y,z)=4x\cos (y-z)(\partial)/(\partial z)(y-z)`

`f_z(x,y,z)=4x\cos (y-z)(-1)`

`f_z(x,y,z)=-4x\cos (y-z)`

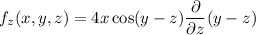
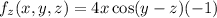
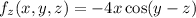
Therefore, the first partial derivatives of the function are
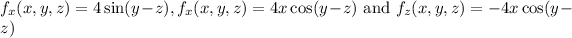`f_x(x,y,z)=4\sin (y-z), f_x(x,y,z)=4x\cos (y-z)\text{ and }f_z(x,y,z)=-4x\cos (y-z)`.