Question

Una lancha que viaja a 10 m/s pasa por debajo de un puente 3 segundos después que ha pasado un bote que viaja a 7 m/s, ¿después de cuántos metros la lancha alcanzará al bote?

Answer 1

La lancha y el bote se encontrarán a 70 metros de distancia del puente.

Explanation:

Sea el punto debajo del puente el punto de referencia y que ambas lanchas se desplazan a velocidad a continuación, las ecuaciones cinemáticas para cada embarcación son presentadas a continuación:

Bote a 7 metros por segundo

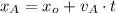`x_(A) = x_(o)+v_(A)\cdot t` (Ec. 1)

Lancha a 10 metros por segundo

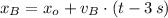`x_(B) = x_(o)+v_(B)\cdot (t-3\,s)` (Ec. 2)

Donde:

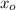`x_(o)` - Posición debajo del puente, medido en metros.

`x_(A)`,
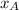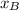`x_(B)` - Posición final de cada embarcación, medido en metros.

`v_(A)`,
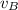`v_(B)` - Velocidad de cada embarcación, medida en metros por segundo.

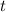`t` - Tiempo, medido en segundos.

Para determinar la posición en la que ambas embarcaciones se encuentran, se debe determinar el instante en que ocurre a partir de la siguiente condición:
`x_(A) = x_(B)`

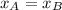
Igualando (Ec. 1) y (Ec. 2) se tiene que:

`v_(A)\cdot t = v_(B)\cdot (t-3\,s)`

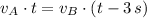
Ahora despejamos el tiempo:

`3\cdot v_(B) = (v_(B)-v_(A))\cdot t`

`t = (3\cdot v_(B))/(v_(B)-v_(A))`

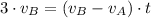
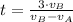
Si sabemos que
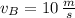`v_(B) = 10\,(m)/(s)` y
`v_(A) = 7\,(m)/(s)`, entonces:

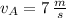`t = (3\cdot \left(10\,(m)/(s) \right))/(10\,(m)/(s)-7\,(m)/(s))`

`t = 10\,s`

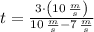
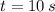
Ahora, la posición de encuentro es: (
`x_(o) = 0\,m`,
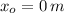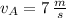`v_(A) = 7\,(m)/(s)` y
`t = 10\,s`)

`x_(A) = 0\,m + \left(7\,(m)/(s) \right)\cdot (10\,s)`

`x_(A) = 70\,m`

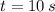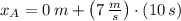
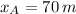
La lancha y el bote se encontrarán a 70 metros de distancia del puente.