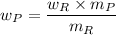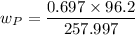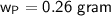Answer:
The yield of the product in gram is
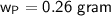
Step-by-step explanation:
Given that:
the molecular mass weight of the product = 96.2 g/mol
the molecular mass of the reagent (3S)-2,2,-dibromo-3,4-dimethylpentane is 257.997 g
given that the millimoles of the reagent = 2,7 millimoles =
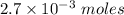
We know that:
Number of moles = mass/molar mass
Then:
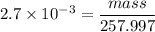
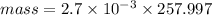
mass = 0.697
Theoretical yield = (number of moles of the product/ number of moles of reactant) × 100
i.e
Theoretical yield =
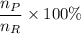
where;
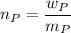 and
and
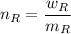
Theoretical yield =
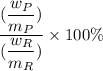
Given that the theoretical yield = 100%
Then:
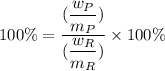
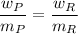
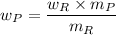
where,
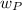 = derived weight of the product
= derived weight of the product
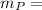 the molecular mass of the derived product
the molecular mass of the derived product
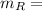 the molecular mass of the reagent
the molecular mass of the reagent
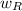 = weight in a gram of the reagent
= weight in a gram of the reagent