Question

Point A is at (-7,5) and point M is at (0.4). Point M is the midpoint of point A and point B. What are the coordinates of point B?​

Answer 1

7,3

Explanation:

Answer 2

The coordinates of point B is

( 7 , 3)

Explanation:

The midpoint M of two endpoints of a line segment can be found by using the formula

`M = ( (x1 + x2)/(2) , \: (y1 + y2)/(2) )`

where

(x1 , y1) and (x2 , y2) are the points

Let the coordinates of B be ( x , y)

From the question the midpoint is ( 0 , 4) and A is (-7 , 5)

So we have

`(0 \: , \: 4) = ( ( - 7 + x)/(2) , \: (5 + y)/(2) )`

Next we compare the x and y coordinates of the midpoint to the x and y coordinates on the right hand side to find the missing coordinates

That's we equate them

So we have

For x

`0 = ( - 7 + x)/(2) \\ - 7 + x = 0 \\ \\ x = 7`

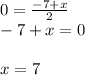
For y

`4 = (5 + y)/(2) \\ 8 = 5 + y \\ y = 8 - 5 \\ \\ y = 3`

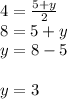
So we have

x = 7 , y = 3

So the coordinates of point B is

( 7 , 3)

Hope this helps you