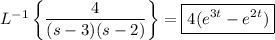I suppose you're asking about the inverse Laplace transform of
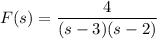
by way of the convolution theorem.
The theorem itself says that
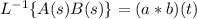
where
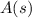 and
and
 are the Laplace transforms of
are the Laplace transforms of
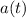 and
and
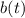 , respectively.
, respectively.
Let
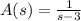 and
and
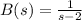 . Then
. Then
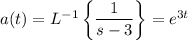

So we have
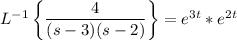
Convolution is defined as
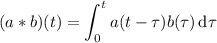
The convolution of
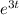 and
and
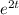 is
is
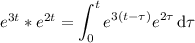
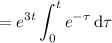

We end up with