Question

How does the graph of f(x) = 1/2(3)x+2 relate to its parent function?

A. The parent function has been translated to the left.
O B. The parent function has been compressed.
OC. The parent function has been stretched.
D. The parent function has been translated down.
SUBM

Answer 1

1) Translated to left by 2 unit.

2) Translated down by 1 unit.

3) Compressed vertically by 1/2 unit.

Explanation:

Given : Graph of the function
`f(x)=(1)/(2)(3)^{x+2`

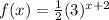
To find : How does f(x) relates to its parent function.

Solution : First we figure out its parent function

Parent function is the simplest form of the function.

f(x) parent function is
`g(x)=3^x`

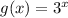
Now, how f(x) relates to g(x)

1. The parent function has been translated to the left.

Translated to left means

f(x)→f(x+b) , graph of f(x) has been translated by b unit.

In g(x)→g(x+2), graph of g(x) has been translated by 2 unit.

→The graph of g(x) has been translated to the left by 2 unit in the graph of f(x).

2)The parent function has been translated to the down.

Translated to down means

f(x)→f(x)-b , graph of f(x) has been translated left by b unit.

In g(x)→g(x)-1, graph of g(x) has been translated down by 1 unit.

→The graph of g(x) has been translated to the down by 1 unit in the graph of f(x).

3)The parent function has been compressed.

Compressed means

f(x)→a g(x) , graph of f(x) has been compressed by a unit.

In g(x)→(1/2)f(x), graph of g(x) has been compressed vertically by 1/2 unit.

→The graph of g(x) has been compressed vertically by 1/2 unit in the graph of f(x).