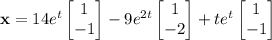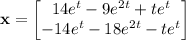Question

Find the unique solution to the following linear system X = (0 -1 2 3)X + (e' -e')
X(0)=(5 4)

Answer 1

It looks like the system is supposed to be

`\mathbf x'=\begin{bmatrix}0&-1\\2&3\end{bmatrix}\mathbf x+\begin{bmatrix}e^t\\e^(-t)\end{bmatrix}`

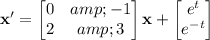
with the initial condition,
`\mathbf x(0)=\begin{bmatrix}5&4\end{bmatrix}^\top`.

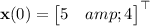Compute the eigensystem for the coefficient matrix:

`\begin{vmatrix}-\lambda&-1\\2&3-\lambda\end{vmatrix}=\lambda^2-3\lambda+2=(\lambda-1)(\lambda-2)=0`

`\lambda_1=1\implies\begin{bmatrix}-1&-1\\2&2\end{vmatrix}\mathbf v_1=\mathbf 0\implies\mathbf v_1=\begin{bmatrix}1\\-1\end{bmatrix}`

`\lambda=2\implies\begin{bmatrix}-2&-2\\2&1\end{bmatrix}\mathbf v_2=\mathbf 0\implies\mathbf v_2=\begin{bmatrix}1\\-2\end{bmatrix}`

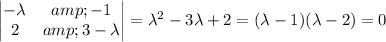
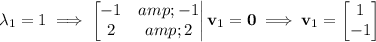
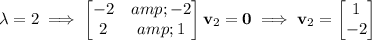
So we have the characteristic solution,

`\mathbf x_c=C_1e^(\lambda_1t)\mathbf v_1+C_2e^(\lambda_2t)\mathbf v_2`

`\mathbf x_c=C_1e^t\begin{bmatrix}1\\-1\end{bmatrix}+C_2e^(2t)\begin{bmatrix}1\\-2\end{bmatrix}`

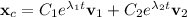
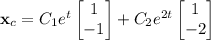
For the non-homogeneous part, we can guess a particular solution of the form

`\mathbf x_p=te^t\begin{bmatrix}a\\b\end{bmatrix}`

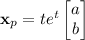
(We might have started with
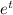`e^t` instead, but that is already accounted for in the first characteristic solution.)

Its derivative is

`{\mathbf x_p}'=e^t\begin{bmatrix}a\\b\end{bmatrix}+te^t\begin{bmatrix}a\\b\end{bmatrix}=e^t\begin{bmatrix}at+a\\bt+b\end{bmatrix}`

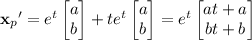
Substitute
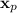`\mathbf x_p` into the system and solve for
`a,b`:

`e^t\begin{bmatrix}at+a\\bt+b\end{bmatrix}=te^t\begin{bmatrix}0&-1\\2&3\end{bmatrix}\begin{bmatrix}a\\b\end{bmatrix}+e^t\begin{bmatrix}1\\-1\end{bmatrix}`

`\begin{bmatrix}at+a\\bt+b\end{bmatrix}=\begin{bmatrix}-bt+1\\(2a+3b)t-1\end{bmatrix}`

`\implies a=1,b=-1`

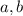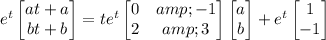
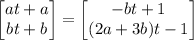
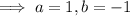
and so the particular solution is

`\mathbf x_p=te^t\begin{bmatrix}1\\-1\end{bmatrix}`

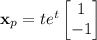
The general solution to the system is then

`\mathbf x=\mathbf x_c+\mathbf x_p`

`\mathbf x=C_1e^t\begin{bmatrix}1\\-1\end{bmatrix}+C_2e^(2t)\begin{bmatrix}1\\-2\end{bmatrix}+te^t\begin{bmatrix}1\\-1\end{bmatrix}`

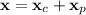
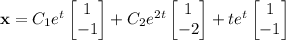
Use the given initial conditions to solve for the remaining coefficients.

`\mathbf x(0)=\begin{bmatrix}5\\4\end{bmatrix}`

`\implies\begin{bmatrix}5\\4\end{bmatrix}=C_1\begin{bmatrix}1\\-1\end{bmatrix}+C_2\begin{bmatrix}1\\-2\end{bmatrix}`

`\implies C_1=14,C_2=-9`

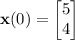
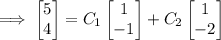
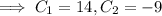
Then the solution to the initial value problem is

`\mathbf x=14e^t\begin{bmatrix}1\\-1\end{bmatrix}-9e^(2t)\begin{bmatrix}1\\-2\end{bmatrix}+te^t\begin{bmatrix}1\\-1\end{bmatrix}`

`\mathbf x=\begin{bmatrix}14e^t-9e^(2t)+te^t\\-14e^t-18e^(2t)-te^t\end{bmatrix}`