Question

If you cannot see the pic:

Points A,B, and C are collinear. Point B is between A and C. Find the length indicated.
BC = x + 15, AC = 14, and AB = x + 7.
Find AB

a) 4
b) 5
c) 3
d) 6​

Answer 1

A. 3

Explanation:

Given,

`BC = x + 15`,

`AC = 14`

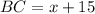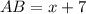`AB = x + 7`, since A, B, and C are collinear, therefore, based on the segment addition postulate:

`AB + BC = AC`.

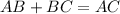Thus, substituting the values into the equation, we have:

`(x + 7) + (x + 15) = 14`

Solve for x.

`x + 7 + x + 15 = 14`

`2x + 22 = 14`

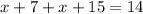
Subtract 22 from both sides

`2x = - 8`

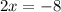
Divide both sides by 2

`x = -4`

`AB = x + 7`

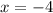
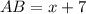
Plug in the value of x

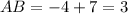`AB = -4 + 7 = 3`,