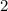Question

HELPPPPP!!!! tHIS IS REALLY HARD!!!!!

Answer 1

Answer: J.

Step-by-step explanation: -tanx i believe

Answer 2

H: 2

Explanation:

`(√(1-\cos ^2\left(x\right)))/(\sin \left(x\right))+(√(1-\sin ^2\left(x\right)))/(\cos \left(x\right))`

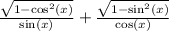
LCM is
`\cos \left(x\right)\sin \left(x\right)`

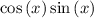
Adjust fractions:

`(√(1-\cos ^2\left(x\right))\cos \left(x\right))/(\sin \left(x\right)\cos \left(x\right))+(√(1-\sin ^2\left(x\right))\sin \left(x\right))/(\cos \left(x\right)\sin \left(x\right))`

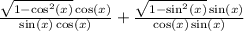
Combine:

`(√(1-\cos ^2\left(x\right))\cos \left(x\right)+√(1-\sin ^2\left(x\right))\sin \left(x\right))/(\sin \left(x\right)\cos \left(x\right))`

--------------------------------------------------------

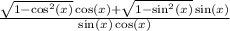
We will take a look at
`√(1-\cos ^2\left(x\right))\cos \left(x\right)`.

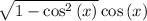Using the identity that
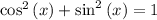`\cos ^2\left(x\right)+\sin ^2\left(x\right)=1`, we know that
`1-\cos ^2\left(x\right)=\sin ^2\left(x\right)`.

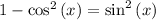Therefore,
`√(1-\cos ^2\left(x\right))\cos \left(x\right)=√(\sin ^2\left(x\right))\cos \left(x\right)=\sin \left(x\right)\cos \left(x\right)`

-----------------------------------------------------------------------------------------------

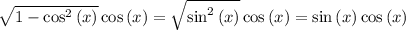
Similarly,
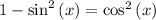`1-\sin ^2\left(x\right)=\cos ^2\left(x\right)` so

`√(1-\sin ^2\left(x\right))\sin \left(x\right)=√(\cos ^2\left(x\right))\sin \left(x\right)=\cos \left(x\right)\sin \left(x\right)`

-------------------------------------------------------------------------------

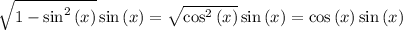
We will finally end up with

`(\sin \left(x\right)\cos \left(x\right)+\cos \left(x\right)\sin \left(x\right))/(\sin \left(x\right)\cos \left(x\right))`

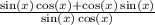
Add:

`(2\sin \left(x\right)\cos \left(x\right))/(\sin \left(x\right)\cos \left(x\right))`

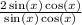
Cancel out sin(x):

`(2\cos \left(x\right))/(\cos \left(x\right))`

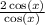
Cancel out cos(x):

`2`