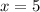Question

Ej bisects def, m dej-5x+7, m JEF=8x-8. find x

Answer 1

`x = 5`

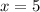
Explanation:

Given that segment EJ bisects angle DEF, it implies that angle DEF is divided into two equal angles, namely, angle DEJ = 5x + 7, and angle JEF = 8x - 8.

To find the value of x, let's derive an equation by setting m<DEJ equal to m<JEF, since both are equal parts of angle DEF bisected by segment EJ.

Thus:

`5x + 7 = 8x - 8`

Solve for x

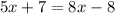
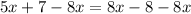`5x + 7 - 8x = 8x - 8 - 8x` (subtracting 8x from both sides)

`-3x + 7 = - 8`

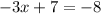
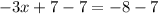`-3x + 7 - 7 = - 8 - 7` (Subtracting 7 from both sides)

`-3x = -15`

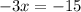
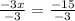`(-3x)/(-3) = (-15)/(-3)` (dividing both sides by -3)

`x = 5`