Question

Prove cos x / 1+sinx = tan ( π\4 - x/2)​

Answer 1

`\displaystyle (\cos x)/(1 + \sin x) = \tan\left((\pi)/(4) - (x)/(2)\right)`.

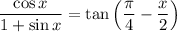Overview of the steps:

• Apply the double-angle identity of sines and cosines to the left-hand side of the equation.
• Apply the Pythagorean identity to the left-hand side of the equation.
• Apply the angle sum and difference identity of sines and cosine to the right-hand side of the equation.

Explanation:

Double-angle identity of sines and cosines:

• 
  `\cos (2\,\alpha) = \cos^2\alpha - \sin^2\alpha = (\cos\alpha + \sin\alpha)\, (\cos\alpha - \sin\alpha)`.
• 
  `\sin(2\,\alpha) = 2\, \sin\alpha\, \cos\alpha`.

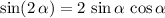Pythagorean identity for the sine and cosine of the same angle:

`1 = \cos^2\alpha + \sin^2\alpha`.

Angle sum and difference identity of sines and cosines:

`\sin(\alpha - \beta) = \sin\alpha\, \cos\beta - \cos\alpha \, \sin\beta`.

`\cos(\alpha - \beta) = \cos\alpha\, \cos\beta + \sin\alpha \, \sin\beta`.

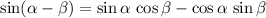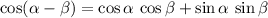Consider
`x` as the sum of two angles of size
`(x/2)`. Start by applying the double-angle identity to the left-hand side.

`\begin{aligned} \text{L.H.S.}&= (\cos(x))/(1 + \sin(x)) \\ &= (\cos^2(x / 2) - \sin^2(x / 2))/(1 + 2\, \sin(x / 2)\, \cos(x / 2))\end{aligned}`.

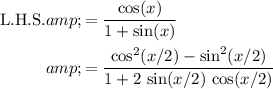Apply the Pythagorean identity to rewrite the "1" in the denominator as
`\left(\cos^2(x / 2) + \sin^2(x / 2)\right)`.

`\begin{aligned} \text{L.H.S.}&= (\cos(x))/(1 + \sin(x)) \\ &= (\cos^2(x / 2) - \sin^2(x / 2))/(1 + 2\, \sin(x / 2)\, \cos(x / 2))\\ &= (\cos^2(x / 2) - \sin^2(x / 2))/(\sin^2(x/2) + 2\,\sin(x/2)\, \cos(x/2) + \cos^2 (x/2))\end{aligned}`.

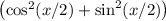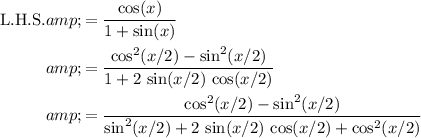Note that the denominator is now a perfect square. On the other hand, the numerator is in the form
`(x^2 - y^2)`, which is equal to
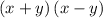`(x + y)\, (x - y)`. Rewrite and simplify this expression:

`\begin{aligned} \text{L.H.S.}&= (\cos(x))/(1 + \sin(x)) \\ &= (\cos^2(x / 2) - \sin^2(x / 2))/(1 + 2\, \sin(x / 2)\, \cos(x / 2))\\ &= (\cos^2(x / 2) - \sin^2(x / 2))/(\sin^2(x/2) + 2\,\sin(x/2)\, \cos(x/2) + \cos^2 (x/2)) \\[1em] &= ((\cos(x/2) + \sin(x/2))\, (\cos(x/2) - \sin(x/2)))/(\left(\sin(x/2) + \cos(x/2)\right)^2) \\ &= (\cos(x/2) - \sin(x/2))/(\sin(x/2) + \cos(x/2))\end{aligned}`.

The tangent of an angle is equal to the ratio between its sine and its cosine. Apply the angle sum and difference identity of sine and cosine to the right-hand side.

Note, that the sine and cosine of
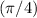`(\pi/4)` are both equal to
`\left(√(2)/2\right)`.

`\begin{aligned}\text{R.H.S.} &= \tan\left((\pi)/(4) - (x)/(2)\right) \\ &= (\sin((\pi/4) - (x/2)))/(\cos((\pi/4) - (x/2)))\\ &= (\left(√(2)/2\right)\, \cos(x/2) - \left(√(2)/2\right)\, \sin(x/2))/(\left(√(2)/2\right)\, \cos(x/2) + \left(√(2)/2\right)\, \sin(x/2)) \\ &= (\cos(x/2) - \sin(x/2))/(\cos(x/2) + \sin(x/2))\end{aligned}`.

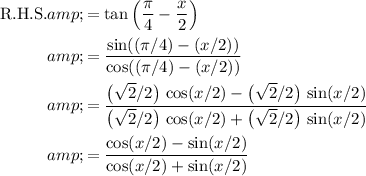Therefore:

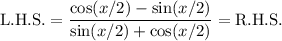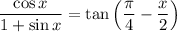`\displaystyle \text{L.H.S.} = (\cos(x/2) - \sin(x/2))/(\sin(x/2) + \cos(x/2)) =\text{R.H.S.}`.

`\displaystyle (\cos x)/(1 + \sin x) = \tan\left((\pi)/(4) - (x)/(2)\right)`.