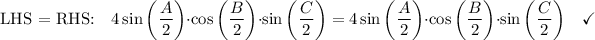Question

Please help me!!!!!​

Answer 1

Answer: see proof below

Explanation:

Given: A + B + C = π → A = π - (B + C)

→ B = π - (A + C)

→ C = π - (A + B)

Use Sum to Product Identity: sin A - sin B = 2 cos [(A + B)/2] · sin [(A - B)/2]

Use the following Cofunction Identity: cos (π/2 - A) = sin A

Proof LHS → RHS:

LHS: sin A - sin B + sin C

= (sin A - sin B) + sin C

`\text{Sum to Product:}\quad 2\cos \bigg((A+B)/(2)\bigg)\cdot \sin \bigg((A-B)/(2)\bigg)+2\cos \bigg(\frac{C}2{}\bigg)\cdot \sin \bigg((C)/(2)\bigg)`

`\text{Given:}\qquad 2\cos \bigg((\pi -(B+C))/(2)+(B)/(2)}\bigg)\cdot \sin \bigg((A-B)/(2)\bigg)+2\cos \bigg(\frac{C}2{}\bigg)\cdot \sin \bigg((C)/(2)\bigg)\\\\\\.\qquad \qquad =2\cos \bigg((\pi -C)/(2)\bigg)\cdot \sin \bigg((A-B)/(2)\bigg)+2\cos \bigg(\frac{C}2{}\bigg)\cdot \sin \bigg((C)/(2)\bigg)`

`.\qquad \qquad =2\cos \bigg((\pi)/(2) -(C)/(2)\bigg)\cdot \sin \bigg((A-B)/(2)\bigg)+2\cos \bigg(\frac{C}2{}\bigg)\cdot \sin \bigg((C)/(2)\bigg)`

`\text{Cofunction:} \qquad 2\sin \bigg((C)/(2)\bigg)\cdot \sin \bigg((A-B)/(2)\bigg)+2\cos \bigg(\frac{C}2{}\bigg)\cdot \sin \bigg((C)/(2)\bigg)`

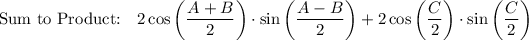
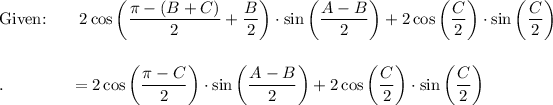
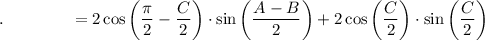
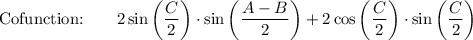
`\text{Factor:}\qquad 2\sin \bigg((C)/(2)\bigg)\bigg[ \sin \bigg((A-B)/(2)\bigg)+\cos \bigg((C)/(2)\bigg)\bigg]`

`\text{Given:}\qquad 2\sin \bigg((C)/(2)\bigg)\bigg[ \sin \bigg((A-B)/(2)\bigg)+\cos \bigg((\pi -(A+B))/(2)\bigg)\bigg]\\\\\\.\qquad \qquad =2\sin \bigg((C)/(2)\bigg)\bigg[ \sin \bigg((A-B)/(2)\bigg)+\cos \bigg((\pi)/(2) -((A+B))/(2)\bigg)\bigg]`

`\text{Cofunction:}\qquad 2\sin \bigg((C)/(2)\bigg)\bigg[ \sin \bigg((A-B)/(2)\bigg)+\sin \bigg((A+B)/(2)\bigg)\bigg]`

`\text{Sum to Product:}\qquad 2\sin \bigg((C)/(2)\bigg)\bigg[ 2\sin \bigg((A)/(2)\bigg)\cdot \cos \bigg((B)/(2)\bigg)\bigg]\\\\\\.\qquad \qquad \qquad \qquad =4\sin \bigg((A)/(2)\bigg)\cdot \cos \bigg((B)/(2)\bigg)\cdot \sin \bigg((C)/(2)\bigg)`

`\text{LHS = RHS:}\quad 4\sin \bigg((A)/(2)\bigg)\cdot \cos \bigg((B)/(2)\bigg)\cdot \sin \bigg((C)/(2)\bigg)=4\sin \bigg((A)/(2)\bigg)\cdot \cos \bigg((B)/(2)\bigg)\cdot \sin \bigg((C)/(2)\bigg)\quad \checkmark`