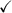Question

Please help me to prove this. ​

Answer 1

For triangle : A + B + C = π

⇒ A + B = π - C

⇒ cot(A + B) = cot(π - C)

⇒
`\sf(cotA\:cotB-1)/(cotB+cotA)=-cotA`

⇒
`\bf{cotA\:cotB+cotB\:cotC+cotC\:cotA=1}`

Now 1st part of the given expression!

⇒
`\sf(cosA)/(sinB\:sinC)`

⇒
`\sf(cos(\pi-(B+C)))/(sinB\:sinC)`

⇒
`\sf(-cosB\:cosC+sinB\:sinC)/(sinB\:sinC)`

⇒ 1 - cotB cotC

Similarly 2nd part!

⇒ 1 - cotA cotB

Similarly 3rd part!

⇒ 1 - cotC cotA

LHS :

`\circ\:\sf{3-(cotA\:cotB+cotB\:cotC+cotC\:cotA)}`

`\circ\:\sf{3-1}`

`\circ\:\bf{2}` = RHS

Hence Proved!!

Answer 2

Answer: see proof below

Explanation:

Given: A + B + C = π → A + B = π - C

→ B + C = π - A

→ A + C = π - B

Use the following Double Angle Identity: sin 2A = 2 sin A · cos A

Use the following Cofunction Identity: sin A = cos (π/2 - A)

Use the following Sum to Product Identity:

sin A + sin B = sin [(A + B)/2] · cos [(A - B)/2]

Proof LHS → RHS

`\text{LHS:}\qquad (\cos A)/(\sin B\cdot \sin C)+(\cos B)/(\sin C\cdot \sin A)+(\cos C)/(\sin A\cdot \sin B)\\\\\\.\qquad \quad = \bigg((2\sin A)/(2\sin A)\bigg)(\cos A)/(\sin B\cdot \sin C)+\bigg((2\sin B)/(2\sin B)\bigg)(\cos B)/(\sin C\cdot \sin A)+\bigg((2\sin C)/(2\sin C)\bigg)(\cos C)/(\sin A\cdot \sin B)\\\\\\.\qquad \quad =(2\sin A\cdot \cos A+2\sin B\cdot \cos B+2\sin C\cdot \cos C)/(2\sin A\cdot \sin B\cdot \sin C)`

`\text{Double Angle:}\qquad \qquad (\sin 2A+\sin 2B+\sin 2C)/(2\sin A\cdot \sin B\cdot \sin C)\\\\\\.\qquad \qquad \qquad \qquad =((\sin 2A+\sin 2B)+\sin 2C)/(2\sin A\cdot \sin B\cdot \sin C)`

`\text{Sum to Product:}\qquad (2\sin (A+B)\cdot \cos (A-B)+\sin 2C)/(2\sin A\cdot \sin B\cdot \sin C)`

`\text{Given:}\qquad \qquad \qquad (2\sin (\pi -C)\cdot \cos (A-B)+\sin 2C)/(2\sin A\cdot \sin B\cdot \sin C)\\\\\\.\qquad \qquad \qquad \qquad =(2\sin C\cdot \cos (A-B)+\sin 2C)/(2\sin A\cdot \sin B\cdot \sin C)`

`\text{Double Angle:}\qquad \qquad (2\sin C\cdot \cos (A-B)+2\sin C\cdot \cos C)/(2\sin A\cdot \sin B\cdot \sin C)\\\\\\.\qquad \qquad \qquad \qquad =(2\sin C(\cos (A-B)+\cos C))/(2\sin A\cdot \sin B\cdot \sin C)`

`\text{Sum to Product:}\qquad (2\sin C(2\cos ((A-B+C)/(2))\cdot \cos ((A-B-C)/(2)))/(2\sin A\cdot \sin B\cdot \sin C)\\\\\\.\qquad \qquad \qquad \qquad =(4\sin C\cdot \cos ((A+C)/(2)-(B)/(2))\codt \cos ((A)/(2)-(B+C)/(2)))/(2\sin A\cdot \sin B\cdot \sin C)`

`\text{Given:}\qquad \qquad (4\sin C((\pi-B)/(2)-(B)/(2))\cdot \cos ((A)/(2)-(\pi -A)/(2)))/(2\sin A\cdot \sin B\cdot \sin C)\\\\\\.\qquad \qquad \qquad =(4\sin C((\pi)/(2)-B)\cdot \cos ((\pi)/(2)-A))/(2\sin A\cdot \sin B\cdot \sin C)`

`\text{Cofunction:}\qquad \qquad (4\sin C\cdot \sin B\sin A)/(2\sin A\cdot \sin B\cdot \sin C)\\\\\\.\qquad \qquad \qquad \qquad =2`

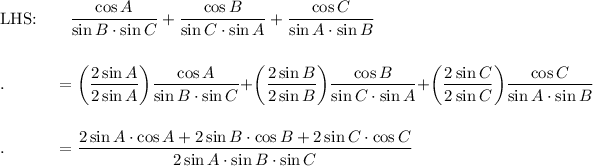
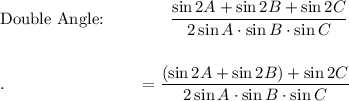
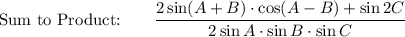
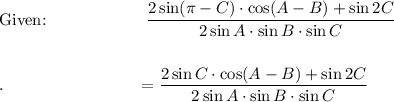
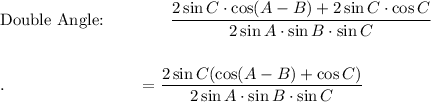
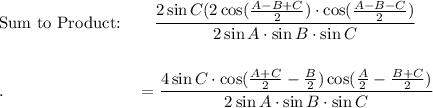
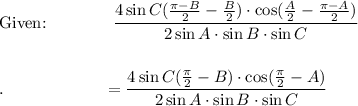
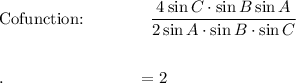
LHS = RHS: 2 = 2
`\checkmark`