Answer:
The equation is missing in the question. The equation is
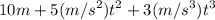
a).
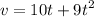 , the horse will not turn.
, the horse will not turn.
b). a(t) = 10 + 18t
Step-by-step explanation:
Given :
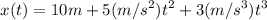
∴ At t =0, x = 10 m
a). Velocity as a function of time
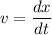
=
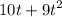
Turning velocity must be zero.
v(t) = 0

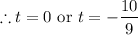
Taking the positive value of time.
The horse will not turn.
b). Acceleration as a function of time.
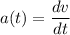
= 10 + 18t
∴ a(t) = 10 + 18t