Answer:
The answer is given below
Explanation:
Z score is used to measure by how many standard deviations the raw score is above or below the mean. It is given by the formula:
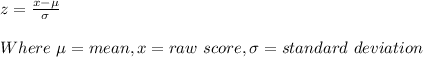
For the male:
μ = 3259.8 g, σ = 869.7 g
Hence for a male who weighs 1600 g, the z score is:

For the female:
μ = 3000.9 g, σ = 550.8 g
Hence for a female who weighs 1600 g, the z score is:
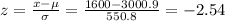
Since the z score for the male is z= -1.91 and the z score for the female is z= -2.54 the male has the weight that is more extreme.