Question

Vector A has a magnitude of 63 units and points west, while vector B has the same magnitude and points due south. Find the magnitude and direction of a) A + B and b) A - B. Specify the directions relative due west.​

Answer 1

Given :

Vector A has a magnitude of 63 units and points west, while vector B has the same magnitude and points due south.

To Find :

The magnitude and direction of

a) A + B .

b) A - B.

Solution :

Let , direction in north is given by +j and east is given by +i .

So ,
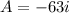`A=-63i` and
`B=63j`

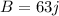
Now , A + B is given by :

`A+B=-63i+63j`

`| A+B | = 63√(2)`

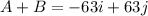
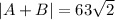
Direction of A+B is 45° north of west .

Also , for A-B :

`A-B=-63i-63j`

`|A-B|=63√(2)`

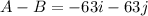
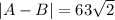
Direction of A-B is 45° south of west .

( When two vector of same magnitude which are perpendicular to each other are added or subtracted the resultant is always 45° from each of them)

Hence , this is the required solution .