Question

# Expand (2x - 3)2. If a, b, and c represent

the coefficients of the resulting polynomial in

descending powers of x, what is a+b+c?

Answer 1

a + b + c = 1

Explanation:

To expand the bracket,
`(2x - 3)^(2)` we will simply be multiplying the bracket by itself.

This will be the same as having
`(2x - 3) * (2x - 3)`

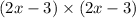
The first step in doing this is to multiply each of the values in the second bracket by the values in the first one.

`2x * 2x =4x^2`

`2x* -3 = -6x`

`-3 * 2x = -6x`

`-3 * -3 =9`

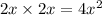
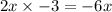
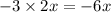
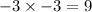
Once this is done, the next step is to group the like terms and evaluate the result.

`4x^2 -6x-6x +9`

`4x^2 -12x +9`

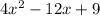
This is algebraic expression is the result of the expansion of
`(2x - 3)^(2)` .

Based on the descending powers of x

a = 4

b = -12

c = 9

These are the coefficients of
`x^2` and
`x` and also the last figure.

a + b + c = 4 -12 +9 = 1