Answer:
The value is
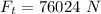
Step-by-step explanation:
From the question we are told that
The flow rate is
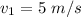
The entrance diameter is
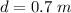
The exit diameter is evaluated as

The entrance gauge pressure is
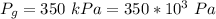
The droped gauge pressure is
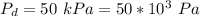
The presure at the exist is evaluated as
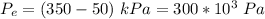
Generally the entrance cross-sectional area is mathematically represented as
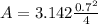
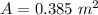
Generally the exit cross-sectional area is mathematically represented as
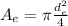
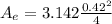
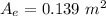
Generally from the continuity equation

=>
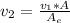
=>

=>
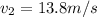
Generally the net force in horizontal axis is equivalent to the net momentum change in the horizontal direction
So
![P_g * A + F_t - P_e * A_e = P_d [ A_e * v_2^2 - A* v_1^2]](https://img.qammunity.org/2021/formulas/physics/college/v6zw4x3nop7ypi8osrh44pih5o8hn7ulr7.png)
Here
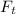 is the horizontal thrust on the fitting
is the horizontal thrust on the fitting
So
![350*10^(3) * 0.385 + F_t -0.385 * 0.139 = 50*10^(3) [ 0.385* 13.8^2 - 0.385* 5^2]](https://img.qammunity.org/2021/formulas/physics/college/co1onl27emphls5zmd9msgenf8rx63zwfj.png)