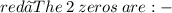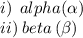Question

# What does it mean if a quadratic polynomial

is prime? Give two examples of quadratic

polynomials that are prime. Now, find a quadratic

polynomial that is prime.

Answer 1

`\huge\sf\underline{\purple{❥}\pink{Q}\orange{U}\blue{E}\red{S}\green{T}\purple{I}\pink{O}\red{N}}`

# What does it mean if a quadratic polynomial

is prime? Give two examples of quadratic

polynomials that are prime. Now, find a quadratic

polynomial that is prime.

`\huge\sf\underline{\purple{❥}\pink{A}\orange {N}\blue{S}\red{W}\green{E}\purple{R}}`

`\color{red}{About \:Quadratic \: polynomials\: :-}`

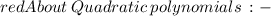
➯ A polynomial having degree 2 is called a quadratic polynomial.

➯ The form of quadratic polynomial is

`p(x) = a {x}^(2) + bx + c`

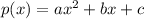
➯ Degree of the quadratic polynomial will be 2.

➯ Variable of the quadratic polynomial will be 1.

`\color{red}{For \:example :-}`

`p(x) = 2 {x}^(2) + 5x + 3 \\ 3 \:➝ \: constant \\ 2 \: and \: 5 \: ➝ \: coefficient \\ {}^(2) \: ➝ \: degree \\ x \:➝ \: variable \:`

➯ In a quadratic polynomial there are 2 zeros because it has degree 2.

`\color{red}{➯ The \: 2\: zeros \:are :-}`

`i) \: \: alpha( \alpha ) \: \\ ii) \: beta \: ( \beta )`

`\color{red}{For \:example :-}`

`p(x) = 2 {x}^(2) + 5 + 3 \\ = 2 {x}^(2) + 2x + 3x + 3 \\ = 2x(x + 1) + 3(x + 1) \\ = (x + 1)(2x + 3) \\ \\ As, \: \: p(x) = 0 \\ \\ ❥∴ \: (x + 1)(2x + 3) = 0 \\ x + 1 = 0 \\ x = - 1 \\ \\ ❥ \: 2x + 3 = 0 \\ 2x = - 3 \\ x = ( - 3)/(2) \\ \\ Here, \: \alpha = - 1 \\ \beta = ( - 3)/(2)`

Answer 2

A quadratic polynomial is a type of polynomial that cannot be factored

Examples are;

x^2 + 3x + 5

x^2 + 5x + 7

Explanation:

A quadratic polynomial is a type of polynomial which cannot be factored. Just like prime numbers, it only has two factors, 1 and itself.

Hence, a quadratic polynomial does not have rational roots. Its roots are complex and not real

Example are as follows;

(i) x^2 + 3x + 5

(ii) x^2 + 5x + 7