Question

Find the midpoint of a segment with the given endpoints.
W(-2,5), X(3,-17) =

Answer 1

The answer is

`( (1)/(2) \: , \: - 6)`

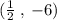
Explanation:

The midpoint M of two endpoints of a line segment can be found by using the formula

`M = ( (x1 + x2)/(2) , \: (y1 + y2)/(2) )`

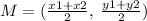
where

(x1 , y1) and (x2 , y2) are the points

From the question the points are

W(-2,5) and X(3,-17)

The midpoint is

`M =( ( - 2 + 3)/(2) , \: (5 - 17)/(2) ) \\ = ( (1)/(2) \: , \: - (12 )/(2) )`

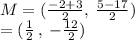
We have the final answer as

`( (1)/(2) \: , \: - 6)`

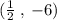
Hope this helps you