Question

A falling object satisfies the initial value problem dv dt = 9.8 − v 5 , v(0) = 0 where v is the velocity in meters per second. (a) Find the time that must elapse for the object to reach 95% of its limiting velocity. (Round your answer to two decimal places.) s (b) How far does the object fall in the time found in part (a)? (Round your answer to two decimal places.) m Additional Materials

Answer 1

a. t
`\simeq` 14.98 sec

b. x = 501.27 m

Step-by-step explanation:

From the given information:

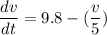`(dv)/(dt)=9.8-((v)/(5 ))` and
`v(0)=0`

`(dv)/(dt)=(49-v)/(5 )`

`(dv)/(49-v)=(dt)/(5 )`

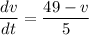
Taking Integral of both sides

`- ln(49-v) = (t)/(5) + C`

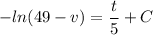
at t=0 we have v=0

This implies that

`- ln(49-0) = (0)/(5) + C`

`C= - ln(49)`

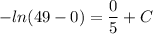
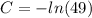
Thus:

`(t)/(5) - In (49) = - In (49 -v) \\ \\ In(49) - (t)/(5) = In (49-v)`

`49-v = e^{(-(t)/(5) +ln(49))}\\ \\ v = 49 - 49e^{(-(t)/(5))}`

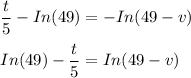
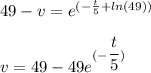
The limiting velocity when the time is infinite is :

95% of 49 = 46.55

∴

`0.05= e^{(-(t)/(5))}`

`(t)/(5)= In((1)/(0.05))`

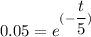
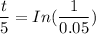
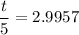
`(t)/(5)=2.9957`

t = 5 × 2.9957

t
`\simeq` 14.98 sec

b.)
`v = 49 - 49e^{(-(t)/(5))}`

`v = (dx)/(dt)=49 - 49e^{(-(t)/(5))}`

`dx=(49 - 49e^{(-(t)/(5))}) \ dt`

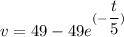
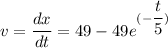
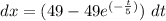
Taking integral of both sides.

`x = 49t + 245 e^{((-t)/(5))} +C`

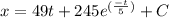
at time t = 0 , distance x traveled = 0

∴

C= - 245

Therefore

`x = 49t + 245 e^{((-t)/(5))} -245`

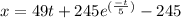
replacing the value of t = 14.98

`x = 49(14.98) + 245 e^{((-14.98)/(5))} -245`

x = 501.27 m