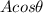What is the xcomponent of A ⃗ x?

Question

asked Nov 21, 2021 163k views

1 Answer

Mhess · Answer 1 · 2021-11-26T03:21:23+0000

Answer:

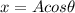
$x = A cos\theta$

Explanation:

Given

Resultant Vector = A

Required

Determine the x component of vector A

To answer this question, I'll make use of the attachment

In the attachment, the relationship between A and the x component is as follows (using Pythagoras theorem):

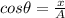
$cos\theta = (x)/(A)$

Multiply both sides by A

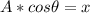
$A * cos\theta = (x)/(A) * A$

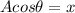
$A * cos\theta = x$

$A cos\theta = x$

Reorder the equation

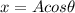
$x = A cos\theta$

Hence, the x component of A is:
$Acos\theta$