Answer: 0.701
Explanation:
Formula :
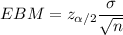 , where
, where
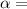 significance level ,
significance level ,
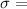 Population standard deviation, n= sample size.
Population standard deviation, n= sample size.
As per given, n= 22
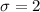
Critical z- value for 90% confidence level :

Then,

Hence , error bound (EBM) of the confidence interval with a 90% confidence level= ± 0.701