Question

Use (a) the midpoint rule and (b) simpson's rule to approximate the below integral. ∫ x^2sin(x) dx with n = 8.

Answer 1

midpoint rule = 5.93295663

simpson's rule = 5.869246855

Explanation:

a) midpoint rule

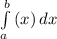`\int\limits^b_a {(x)} \, dx`≈ Δ x (f(x₀+x₁)/2 + f(x₁+x₂)/2 + f(x₂+x₃)/2 +...+ f(x
`_(n)`_₂+x
`_(n)`_₁)/2 +f(x
`_(n)`_₁+x
`_(n)`)/2)

Δx = (b − a) / n

We have that a = 0, b = π, n = 8

Therefore

Δx = (π − 0) / 8 = π/8

Divide the interval [0,π] into n=8 sub-intervals of length Δx = π/8 with the following endpoints:

a=0, π/8, π/4, 3π/8, π/2, 5π/8, 3π/4, 7π/8, π = b

Now, we just evaluate the function at these endpoints:

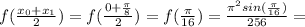`f((x_(0)+x_(1) )/(2) ) = f((0+(\pi)/(8) )/(2) ) = f((\pi )/(16))=(\pi^(2)sin((\pi )/(16)) )/(256) =` 0.00752134

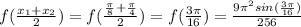`f((x_(1)+x_(2) )/(2) ) = f(((\pi )/(8) +(\pi)/(4) )/(2) ) = f((3\pi )/(16))=(9\pi ^(2) sin((3\pi )/(16)) )/(256)` = 0.19277080

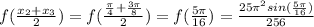`f((x_(2)+x_(3) )/(2) ) = f(((\pi )/(4) +(3\pi)/(8) )/(2) ) = f((5\pi )/(16))=(25\pi ^(2) sin((5\pi )/(16)) )/(256)` = 0.80139415

`f((x_(3)+x_(4) )/(2) ) = f(((3\pi )/(8) +(\pi)/(2) )/(2) ) = f((7\pi )/(16))=(49\pi ^(2) sin((7\pi )/(16)) )/(256)` = 1.85280536

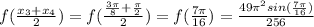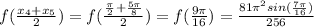`f((x_(4)+x_(5) )/(2) ) = f(((\pi )/(2) +(5\pi)/(8) )/(2) ) = f((9\pi )/(16))=(81\pi ^(2) sin((7\pi )/(16)) )/(256)` = 3.062800704

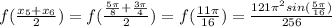`f((x_(5)+x_(6) )/(2) ) = f(((5\pi )/(8) +(3\pi)/(4) )/(2) ) = f((11\pi )/(16))=(121\pi ^(2) sin((5\pi )/(16)) )/(256)` = 3.878747709

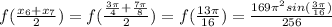`f((x_(6)+x_(7) )/(2) ) = f(((3\pi )/(4) +(7\pi)/(8) )/(2) ) = f((13\pi )/(16))=(169\pi ^(2) sin((3\pi )/(16)) )/(256)` = 3.61980731

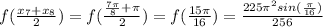`f((x_(7)+x_(8) )/(2) ) = f(((7\pi )/(8) +\pi )/(2) ) = f((15\pi )/(16))=(225\pi ^(2) sin((\pi )/(16)) )/(256)` = 1.69230261

Finally, just sum up the above values and multiply by Δx = π/8:

π/8 (0.00752134 +0.19277080+ 0.80139415 + 1.85280536 + 3.062800704 + 3.878747709 + 3.61980731 + 1.69230261) = 5.93295663

b) simpson's rule

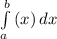`\int\limits^b_a {(x)} \, dx` ≈ (Δx)/3 (f(x₀) + 4f(x₁) + 2f(x₂) + 4f(x₃) + 2f(x₄) + ... + 2f(
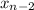`x_(n-2)`) + 4f(
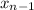`x_(n-1)`) + f(
`x_(n)`))

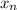where Δx = (b−a) / n

We have that a = 0, b = π, n = 8

Therefore

Δx = (π−0) / 8 = π/8

Divide the interval [0,π] into n = 8 sub-intervals of length Δx = π/8, with the following endpoints:

a = 0, π/8, π/4, 3π/8, π/2, 5π/8, 3π/4, 7π/8 ,π = b

Now, we just evaluate the function at these endpoints:

f(x₀) = f(a) = f(0) = 0 = 0

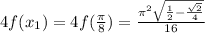`4f(x_(1) ) = 4f((\pi )/(8) )=\frac{\pi^(2)\sqrt{(1)/(2)-(√(2) )/(4) } }{16}` = 0.23605838

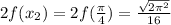`2f(x_(2) ) = 2f((\pi )/(4) )=\frac{\sqrt{2\pi^(2) } }{16}` = 0.87235802

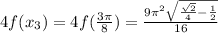`4f(x_(3) ) = 4f((3\pi )/(8) )=\frac{9\pi^(2)\sqrt{(√(2) )/(4)-\frac{{1} }{2} } }{16}` = 5.12905809

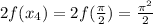`2f(x_(4) ) = 2f((\pi )/(2) )=(\pi ^(2) )/(2)` = 4.93480220

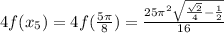`4f(x_(5) ) = 4f((5\pi )/(8) )=\frac{25\pi^(2)\sqrt{(√(2) )/(4)-\frac{{1} }{2} } }{16}` = 14.24738359

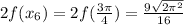`2f(x_(6) ) = 2f((3\pi )/(4) )=\frac{9\sqrt{2\pi^(2) } }{16}` = 7.85122222

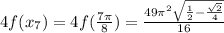`4f(x_(7) ) = 4f((7\pi )/(8) )=\frac{49\pi^(2)\sqrt{(1)/(2)-(√(2) )/(4) } }{16}` = 11.56686065

f(x₈) = f(b) = f(π) = 0 = 0

Finally, just sum up the above values and multiply by Δx/3 = π/24:

π/24 (0 + 0.23605838 + 0.87235802 + 5.12905809 + 4.93480220 + 14.24738359 + 7.85122222 + 11.56686065 = 5.869246855