Consider a triangle ΔABC, where sides AB, BC and angle ∡C are given.
Angle ∡C is the angle opposite of side AB.
It says that the given side opposite the given angle is less than the other given side. It means AB < BC.
It says that the ratio of the longer side to the shorter side, multiplied by the sine of the angle opposite the shorter side, is less than 1. It means
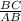 · sin(C) < 1
· sin(C) < 1
We know about Law of Sines of Triangle is given by :-
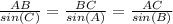
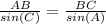
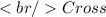
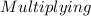
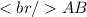
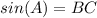
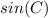
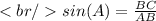
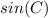
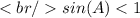 \\
\\
We got sin(A) < 1, and BC > AB.
Therefore, angle ∡A could be either acute or obtuse angle.
So, There will be two solutions for the angle ∡A.
⇒ option D is the final answer.