Answer:
in all three cases the total moment is zero
cases A and B the kinetic energy is conserved.
In case C the velocity decreases so the kinetic energy decreases
Step-by-step explanation:
This is a momentum conservation exercise
p = mv
In order for the moment to be preserved, we must define a system formed by the two cars, so that the forces during coke have been internal.
Before crash
car 1 p₀₁ = m v₀
car 2 p₀₂ = - mv₀
pose us several situations, we analyze each one
A) After the crash the cars stop
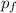 = 0
= 0
p₀₁ m v₀
p₀₂ -m v₀
p_{f} 0
B) After the collision, each vehicle reverses its direction
p₀₁ m v₀
p₀₂ -m v₀
p_{f1} -m v₀
p_{f2} m v₀
C) In this case some of the kinetic energy is lost which is converted into internal energy, for example, deformation, heat, friction.
Consequently the speed of the cars is
v < v₀
p₀₁ m v₀
p₀₂ - m v₀
p_{f1} -m v
p_{f2} m v
D) in cases A and B the momentum is maintained, but in case C the total momentum is maintained, even when the speed of the cars decreases, this is pf_total = 0
In all cases the total impulse is zero
p₀ = p₀₁ + p₀₂ = m v₀ - mv₀
p₀_total = 0
in all three cases the total moment is zero
E) The total kinetic energy is the sum of the kinetic energy of each car
K_total = K₀₁ + K₀₂
K_total = ½ m v₀² + ½ m (-v₀)²
K_total = m v₀²
we see that because it is squared, the sign of the velocity does not matter, therefore in cases A and B the kinetic energy is conserved.
In case C the velocity decreases so the kinetic energy decreases
Kf_total < K₀_total
the missing energy is transformed into internal energy during sackcloth.
In the attachment we can see a vector diagram of the momentum in each case