Answer:
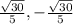
Explanation:
We have the equation

Since we know that any number multiplied by 0 is 0, we can safely make the term
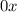 to add to this.
to add to this.
So our equation now is
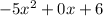
We can now solve for this using the quadratic formula, which is
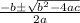 .
.
b is the coefficient on the x term, a is the coefficient on the
 term, and c is the constant.
term, and c is the constant.
Let's substitute inside the equation, since we know
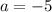 ,
,
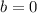 and
and
 .
.
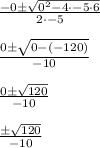
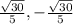
Hope this helped!