Question

A transverse sinusoidal wave is moving along a string in the positive direction of an x axis with a speed of 89 m/s. At t = 0, the string particle at x = 0 has a transverse displacement of 4.2 cm from its equilibrium position and is not moving. The maximum transverse speed of the string particle at x = 0 is 16 m/s. (a) What is the frequency of the wave? (b) What is the wavelength of the wave? If the wave equation is of the form y(x, t) = ym sin(kx ± ωt + φ), what are (c) ym, (d) k, (e) ω, (f) φ, and (g) the correct choice of sign in front of ω?

Answer 1

The answer is below

Step-by-step explanation:

Given that:

y = transverse displacement = 4.2 cm = 0.042 m at x = 0 and t = 0.

Speed = v = 89 m/s, maximum transverse speed of the string particle =
`u_m` = 16 m/s.

ω =
`u_m` /
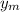`y_m` = 16 / 0.42 = 380.95 rad/s

a) Frequency = ω/2π = 380.95 / 2π = 60.63 Hz

b) Wavelength (λ) = speed / frequency

λ = v / f = 89/63.66= 1.468 m

c) Using the wave equation:

`y=y_msin(kx \pm wt \pm \phi)\\y=0.042,t=0,x=0\\\\Hence\\y_m=0.042\ m`

d) Wave number k is given by:

k = 2π / λ = 2π / 1.468 = 4.28 rad/s

e) The angular velocity is given by:

ω =
`u_m` /
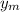`y_m` = 16 / 0.42 = 380.95 rad/s

f) Using the wave equation:

`y=y_msin(kx \pm wt \pm \phi)\\\\y=0.042,t=0,x=0,y_m=0.042\\\\Hence\\0.042=0.042sin(4.28(0)\pm 380.95(0)\pm \phi)\\\\sin\phi=1\\\\\phi=(\pi)/(2) \\\\y=0.042sin(4.28x\pm 380.95t\pm (\pi)/(2))`

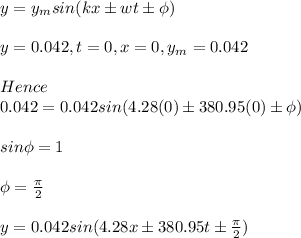
g) Since the wave is in the positive x direction, hence ω is negative