Question

Suppose that 10.0 mol C2H6(g) is confined to 4.860 dm3 at 27 °C. Predict the pressure exerted by the ethane from (i) the perfect gas and (ii) the van der Waals equations of state. Calculate the compression factor based on these calculations. For ethane, a = 5.507 dm6 atm mol−2, b = 0.0651 dm3 mol−1.

Answer 1

`P=35.16`

`Z=4.6`

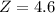
Step-by-step explanation:

Hello,

In this case, since the VdW equation is:

`P=(nRT)/(V-n*b)-a((n)/(V) )^2`

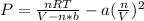
Since the moles are 10.0 moles, the temperature in K is 300.15 K and the volume is liters is also 4.860 L (1 dm³= 1L), the pressure exerted by the ethane is:

`P=(10.0mol*0.082(atm*L)/(mol*K)*300.15K)/(4.860mol-10.0mol*0.0651(L)/(mol) )-5.507(atm*L^2)/(mol^2)((10.0mol)/(4.86L) )^2\\\\P=58.48atm-23.3atm\\\\P=35.16`

Thus the compression factor turns out:

`Z=(PV)/(RT)=(23.3atm*4.86L)/( 0.082(atm*L)/(mol*K)*300.15K)\\\\Z=4.6`

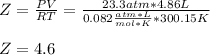
Regards.