Complete Question
The complete question is shown on the first uploaded image
Answer:
the compass direction of the resultant displacement is
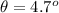 south of west
south of west
Step-by-step explanation:
Generally using cosine we can obtain the resultant R as follows
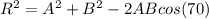
=>
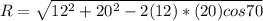
=>
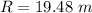
We can obtain the direction of the resultant by first using sine rule to obtain angle C as follows
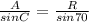
=>
![C= sin ^(-1) [(A * (sin 70))/(R) ]](https://img.qammunity.org/2021/formulas/physics/college/i7idkts2mzbjak2ejp3mxjf5pmb3lahpwi.png)
=>
![C = sin ^(-1) [(20 * (sin 70))/(19.48) ]](https://img.qammunity.org/2021/formulas/physics/college/4nfl86s8qoix0m44qhj92a57rc112oy7pj.png)
=>

Then the direction is obtained as

=>
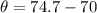
=>
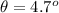
Hence the compass direction of the resultant displacement is
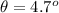 south of west
south of west