Question

Show that a tilted linearly polarized wave can be written as the sum of LCR and RCP.

Answer 1

E_{z} = E_{z} (RCP) + E_{z} (LCP)

E_{z} = 2 E₀ cos (kz-wt) i^

Step-by-step explanation:

An electromagnetic wave is said to be polarized if the electric field for a fixed point in space has a definite direction in time.

Based on this definition we can define some types of polarization; Linear; right-hand, left-hand circular, and elliptical

Circular polarization is that for a fixed point in space, the electric field describes a circle in time, if this circle rotates clockwise it is called right circular polarization (RCP) and if it rotates counterclockwise it is called polarization left circular (LCP)

For wave moving in the z direction the electric fields must oscillate in the x or y direction

for right-hand circular polarization (RCP)

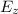`E_(z)` = E₀ cos (kz -wt) i^ + E₀ sin (kz -wt) j^

for left circular polarization (LCP)

E_{z} = E₀ cos (kz -wt) i ^ - E₀ sint (kz -wt) j ^

linear polarization can be obtained if we add these two polarizations

E_{z} = Ez (RCP) + Ez (LCP)

E_{z} = E₀(cos (kz -wt) i^ + sint (kz -wt) j^ + cos (kz -wt) i^ - snt (kz -wt)j^ )

E_{z} = 2 E₀ cos (kz-wt) i^

the latter is a linear polarization on the x axis