Question

What is the axis of symmetry, vertex and y intercept for 2x^2-8x-5

Answer 1

Axis of symmetry: x = 2

Vertex at: (2, -13)

y-intercept is (0, -5)

Explanation:

The equation for the x-value of the vertex in a quadratic of the form:

`y=ax^2+bx+c`

is given by:

`x_(vert)=-(b)/(2\,a)`

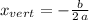
which in our case gives:

`x_(vert)=(8)/(2*2) =2`

Then the equation for the axis of symmetry is given by: x = 2

and the y of the vertex can be calculated as:

`y_(vert)=2 (2)^2-8\,(2)-5=-13`

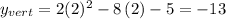
Then the vertex is at the point: (2, -13)

And the y-intercept is found when x=0, that is:

y-intercept is (0, -5)