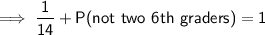Answer:

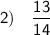
Explanation:
Given:
- 6 sixth graders
- 7 seventh graders
- 8 eight graders
Total = 6 + 7 + 8 = 21

Question 1
The probability of the 1st pick being a 6th grader:

Now there will be 5 sixth graders left and a total of 20 left.
So, the probability of the 2nd pick being a 6th grader:

Therefore,
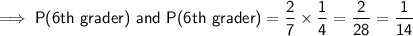
Question 2
Law of Total Probability states that the sum of probabilities is 1