Question

On a 210-mile trip, Cameron drove at an average speed of 60 miles per hour for the first x hours. He then

completed the trip, driving at an average speed of 50 miles per hour for the remaining y hours. If x = 1,
what is the value of y?
y =

Answer 1

`y = 3`

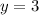
Explanation:

Given

Trip = 250 miles

Speed for first x hours = 60 miles/hour

Speed for next y hours = 50 miles/hour

x = 1

Required

Find y

To solve this question, we'll make use of:

`Distance = Speed * Time`

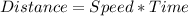
For x hours:

`Distance = 60miles/hour * x`

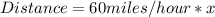
Substitute 1 hour for x

`Distance = 60\ miles/hour * 1\hour`

`Distance = 60\ mile`

For y hours:

`Distance = 50\ miles/hour * y\ hours`

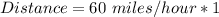
`Distance = 50y\ miles`

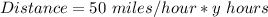
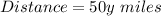
Given that total distance is 210 miles;

We have that:

`Total Distance = 60\ miles + 50y\ miles`

`210\ miles = 60\ miles + 50y\ miles`

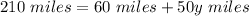
Solve for y

`210 - 60 = 50y`

`150 = 50y`

`y = (150)/(50)`

`y = 3`

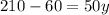
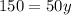
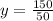
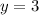
Hence,

y = 3 hours