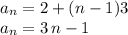Question

The first term of an arithmetic sequence is 2 and the fourth term is 11

Answer 1

The sequence has common difference 3, and its general nth term can be written as:

`a_n=3\,n-1`

Explanation:

In order to define the sequence, we recall the formula for the nth term of an arithmetic sequence as:

`a_n=a_1+(n-1)\,d`

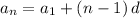
where "d" is the common difference for the sequence (our unknown in this case), and the nth term is our fourth term (n = 4) which equals 11, and the first term is 2:

`a_n=a_1+(n-1)\,d\\11=2+(4-1)\,d\\9=3\,d\\d=9/3\\d=3`

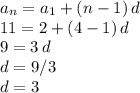
Therefore our sequence has common difference 3, and its general nth term can be written as:

`a_n=2+(n-1)3\\a_n=3\,n-1`