Question

Find the sample standard deviation:

2 6 15 9 11 22 1 4 8 19
A) 6.3.
B) 7.1.
C) 6.8.
D) 2.1

Answer 1

B. 7.1

Explanation:

Given the sample data 2 6 15 9 11 22 1 4 8 19, before we can get the standard deviation, we need to first calculate the mean.

mean = 2 +6 +15 +9 +11 +22 +1 +4 +8 +19/10

mean = 97/10

mean = 9.7

Standard deviation for ungrouped data is expressed using the formula;

`S = \sqrt{ (\sum(x-\overline x)^2)/(n-1) }`

`\overline x \ is\ the \ mean\\n \ is \ sample \ size`

`S = \sqrt{((2-9.7)^2+(6-9.7)^2+(15-9.7)^2+(9-9.7)^2+(11-9.7)^2+(22-9.7)^2+(1-9.7)^2+(4-9.7)^2+(8-9.7)^2+(19-9.7)^2)/(10-1) }\\ S = \sqrt{((-7.7)^2+(-3.7)^2+(5.3)^2+(-0.7)^2+(1.3)^2+(12.3)^2+(-8.7)^2+(-5.7)^2+(-1.7)^2+(9.3)^2)/(10-1) }\\\\S = \sqrt{(59.29+13.69+28.09+0.49+1.69+151.29+75.69+32.49+2.89+86.49)/(10-1) }\\\\\\S = \sqrt{(452.1)/(9) }\\\\S = √(50.23)\\ \\S = 7.08\\\\S \approx 7.1`

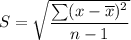
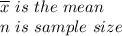
Hence the standard deviation of the sample data is 7.1