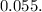Answer:
Explanation:
Let
 be the probability of lying an applicant, so,
be the probability of lying an applicant, so,
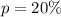 .
.
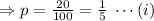
Any applicant will either lie or will tell the truth.
Let
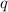 be the probability of telling the truth, so,
be the probability of telling the truth, so,

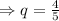
As for every applicant
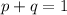 , so this is Bernoullies trials, for which
, so this is Bernoullies trials, for which
the probability of success of exactly
 times of an event out of
times of an event out of
 trials is
trials is
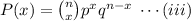 .
.
Now, let
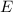 be the event of at least one of the applicants is lying out of
be the event of at least one of the applicants is lying out of
 applicants, here the total number of applicants,
applicants, here the total number of applicants,
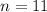 .
.
So,
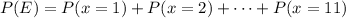
This is equivalent to
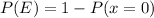 as
as
![[P(x=0)+P(x=1)+ P(x=2)+\cdots+ P(x=11)=1]](https://img.qammunity.org/2021/formulas/mathematics/college/a1akvywdy0tgqkdojogaxc0vwcjispbbji.png)
Now, from equation (iii),
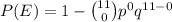
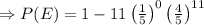 [from equations s (i) and (ii)]
[from equations s (i) and (ii)]
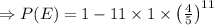
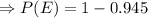 (approx)
(approx)

Hence, the probability that the lie detector indicates that at least one of the applicants is lying is