Answer:
The cost function for
 is
is
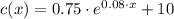 .
.
Explanation:
The marginal cost function (
 ) is the derivative of the cost function (
) is the derivative of the cost function (
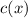 ), then, we should integrate the marginal cost function to find the resulting expression. That is:
), then, we should integrate the marginal cost function to find the resulting expression. That is:

Where:
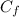 - Fixed costs, measured in US dollars.
- Fixed costs, measured in US dollars.
If we know that
 and
and
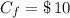 , then:
, then:

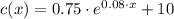
The cost function for
 is
is
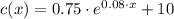 .
.